Simscape Multibodyを使ってフライホイール倒立振子のシミュレーション
この記事はMATLAB/Simulink Advent Calendar 2021 の22日目の記事です.前日は@shinji00qさんによるSimulinkで始める線形システムのモデル規範適応制御(MRAC)の記事でした.
本記事はSimscape Multibodyでフライホイール倒立振子を倒立させるシミュレーションをする話を書きます. どうやって制御したかはもちろんですが,Simscape Multibodyはこんなときに便利なんだなぁとわかった気がするので,そこらへんもまとめていきたいと思います. 筆者は制御初心者ですので間違いや曖昧な点があるかもしれません.ご了承ください. あくまでも制御初心者がSimscape Multibodyという便利なツールを使って,フライホイール倒立振子を倒立させることができたというお話です.
制御対象
以下のようなモデルを倒立させることを考えます.棒の先端に回転する円盤がついていて,円盤を回転させた際に発生する反トルクで棒を倒立させます.円盤はフライホイールと呼ぶことにします. 正確にはリアクションホイールのような気もしますが,とりあえずフライホイールでいいでしょう(多分).

各パラメータは次の表の通りです.$\theta_{1}$と$\theta_{2}$を0にするように制御をします.
| 記号 | 単位 | 説明 |
| $L$ | [m] | 振子の回転軸からホイールの回転軸までの長さ |
| $L_{g}$ | [m] | 振子の回転軸から振子の重心までの長さ |
| $m_{1}$ | [kg] | 振子の重量 |
| $m_{2}$ | [kg] | フライホイールの重量 |
| $c_{1}$ | [Nm rad / s] | 振子の回転軸の粘性係数 |
| $c_{2}$ | [Nm rad / s] | フライホイールの回転軸の粘性係数 |
| $\theta_{1}$ | [rad] | 振子の角度 |
| $\theta_{2}$ | [rad] | フライホイールの角度 |
| $r$ | [m] | フライホイールの半径 |
運動方程式の導出
そこそこ複雑な運動をするので、直接運動方程式を導出するのは骨が折れそうです。そこで、ラグランジアンを使ったラグランジュの運動方程式で導出します。 これは、運動エネルギと位置エネルギの関係から比較的容易に運動方程式を求めることができるものです。 具体的には、振子とフライホイールそれぞれの運動エネルギ$K$と位置エネルギ$U$を求めて、ラグランジアン$L = K - U$を求めてごにょごにょすると運動方程式が計算できます。 ごにょごにょの部分はMATLABがやってくれるので,考えないことにします.振子の運動エネルギ
並進方向と回転方向の運動エネルギを足し合わせて振子の運動エネルギを計算します.まず振子の並進方向の運動エネルギを求めて,次に振子の回転方向の運動エネルギを求めます.
並進方向の運動エネルギの式は$K_{t} = \frac{1}{2} m \dot x^2$が基本です.これを振子に当てはめます。この式の変数は$\dot x^2$ のみなので、こいつを既知のパラメータから求める必要があります。流れとしては、振子の重心の位置を求めてそれを時間微分して速度を求めます。
まず重心の位置は$(x_{g1}, y_{g1})$として,次のように計算できます. \begin{align} x_{g1} = L_{g} sin \theta_{1} \\ y_{g1} = L_{g} cos \theta_{1} \end{align}
次に,これらを時間微分すると次のようになります. \begin{align} \dot x_{g1} = L_{g} \dot \theta_{1} cos \theta_{1} \\ \dot y_{g1} = -L_{g} \dot \theta_{2} sin \theta_{1} \end{align}
最後に,$K_{t} = \frac{1}{2} m \dot x^2$の式に$\dot x_{g1}$と$\dot y_{g1}$を入れて整理すると,次のようになります. \begin{align} K_{rod_{t}} = \frac{1}{2}m_{1}(\dot x_{g1}^2 + \dot y_{g1}^2) \end{align} これで振子の並進方向の運動エネルギ$K_{rod_{t}}$の式が得られました.
回転方向のエネルギは$K_{w} = I \dot \theta^2$が基本です.これを振子に当てはめます.これは特に難しいことはなくすべて既知のパラメータなので,そのまま代入して次のようになります. \begin{align} K_{rod_{w}} = \frac{1}{2}I_{1}\dot \theta_{1}^2 \end{align}
ここで,$I_{1}$はフライホイールの慣性モーメントで,次の式で計算できます. \begin{align} I_{1} = \frac{1}{12}m_{1}L^2 \end{align} これで振子の回転方向の運動エネルギ$K_{rod_{w}}$の式が得られました.
フライホイールの運動エネルギ
振子と同様に、並進方向と回転方向の運動エネルギを足し合わせてフライホイールの運動エネルギを計算します。 まずフライホイールの並進方向の運動エネルギを求めて,次にフライホイールの回転方向の運動エネルギを求めます.
振子と同じような手順で計算していきます.フライホイールの重心位置$(x_{g2}, y_{gs})$は次のようになります. \begin{align} x_{g2} = L sin \theta_{1} \\ y_{g2} = L cos \theta_{1} \end{align}
これを時間微分して,速度は次のようになります. \begin{align} \dot x_{g2} = L \dot \theta_{1} cos \theta_{1} \\ \dot y_{g2} = -L \dot \theta_{2} sin \theta_{1} \end{align}
最後に運動エネルギの式に代入して,次にようになります. \begin{align} K_{wheel_{t}} = \frac{1}{2}m_{2}(\dot x_{g2}^2 + \dot y_{g2}^2) \end{align}
これでフライホイールの並進方向の運動エネルギ$K_{wheel_{t}}$の式が得られました.
フライホイールの回転は、振子自身の回転とフライホイールの回転がたし合わさった回転になります。これを考慮して回転エネルギの式は以下のようになります。 \begin{align} K_{wheel_{w}} = \frac{1}{2}I_{2}(\dot \theta_{1}^2 + \dot \theta_{2}^2) \end{align}
ここで$I_{2}$はフライホイールの慣性モーメントで,次の式で計算できます. \begin{align} I_{2} = \frac{1}{2}m_{2}r^2 \end{align}
これでフライホイールの回転方向の運動エネルギ$K_{wheel_{w}}$の式が得られました.
振子の位置エネルギ
運動エネルギの式は導出はできたので,次は振子とフライホイールの位置エネルギの式を導出します.まず振子の位置エネルギの式を導出します.
振子の位置エネルギーは簡単です。$U = mgh$の式に代入するだけです。$y_{g1}$は運動エネルギの式を導出したときに計算したので,それを使います. \begin{align} U_{rod} = m_{1} g y_{g1} \end{align}
フライホイールの位置エネルギ
次にフライホイールの位置エネルギの式を導出します.フライホイールの位置エネルギーも振子のときとほぼ同じです. $y_{g2}$も運動エネルギの式を導出したときに計算したので,それを使います. \begin{align} U_{wheel} = m_{2} g y_{g2} \end{align}
ラグランジュの運動方程式
今まで計算したエネルギの式を使って,ラグランジアン$L$を導出します.ラグランジアンは運動エネルギと位置エネルギの差で,$L = K - U$になります. 運動エネルギは振子とフライホイールの並進と回転のエネルギをすべて足し合わせて、位置エネルギも振子とフライホイールを両方を足し合わせたものを使用します。 具体的には、次のような式になります。 \begin{align} L = (K_{rod_{t}} + K_{rod_{w}} + K_{wheel_{t}} + K_{wheel_{w}}) - (U_{rod} + U_{wheel}) \end{align}
この$L$を下の式のように偏微分すると運動方程式が計算できます。これがラグランジュの運動方程式と言うらしいです. $x$は任意の変数で、今回は$\theta_{1}$と$\theta_{2}$を代入します。変数が2つあるので式は2つできます。 \begin{align} \frac{d}{d t}\left(\frac{\partial L}{\partial \dot{x}}\right)-\frac{\partial L}{\partial x} = 0 \end{align}
MATLABでラグランジュの運動方程式を導出する
あとはラグランジュの運動方程式を計算すればよいのですが,手計算では間違える自信があるのでMATLABに解いてもらいます. 具体的にはこのスクリプトで解くことができます.最後に回転軸の粘性要素を無理やり追加しています. 粘性のエネルギも導出してラグランジアンに組み込むと一緒に計算してくれるらしい(多分)のですが,うまくできていないので今回はこのような方法をとっています. また,このままだと$sin\theta_{1}$が入ってしまっているので非線形です. これを線形にするために,倒立状態では$\theta_{1}$が限りなく0に近いとして,$sin\theta_{1}$を$\theta_{1}$に近似して線形化しています.
これで次のような式を得ることができます.式が複雑で長いのは整理していないからだと思います. \begin{align} \ddot\theta_{1} =\frac{\mathrm{Tw}-c_{1}\,\dot\theta_{1}+c_{2}\,\dot\theta_{2}+g\,\theta_{1}\,\left(L\,m_{2}+L_{g}\,m_{1}\right)}{m_{2}\,L^2+m_{1}\,{L_{g}}^2+I_{1}} \end{align} \begin{align} \ddot \theta_{2}=-\frac{\mathrm{Tw}-c_{1}\,\dot\theta_{1}+c_{2}\,\dot \theta_{2}+g\,\theta_{1}\,\left(L\,m_{2}+L_{g}\,m_{1}\right)+\frac{I_{1}\,\left(c_{2}\,\dot \theta_{2}+\mathrm{Tw}\right)}{I_{2}}+\frac{L^2\,m_{2}\,\left(c_{2}\,\dot \theta_{2}+\mathrm{Tw}\right)}{I_{2}}+\frac{{L_{g}}^2\,m_{1}\,\left(c_{2}\,\dot \theta_{2}+\mathrm{Tw}\right)}{I_{2}}}{m_{2}\,L^2+m_{1}\,{L_{g}}^2+I_{1}} \end{align}
Simscape Multibodyで運動方程式の妥当性を確認
ここまでで運動方程式を導出しましたが,「本当にこれで正しいのか??」と不安になる方がいるかもしれません.少なくとも筆者はなりました. というのも,運動方程式が正しいか不安なまま制御設計に進むと,うまく制御できなかったときに制御設計が悪いのか運動方程式が悪いのかの判断がつかないな~という思いがありました. そこで活躍するのがSimscape Multibodyです.Simscape Multibodyは物理的なパラメータ(重さや長さなど)を入力しながらモデルをレゴブロックのように組み立ててシミュレーションをすることができます. つまり,運動方程式がなくてもどのような運動をするか完璧にわかるのです!! そこで,導出した運動方程式を数値シミュレーションした結果と,Simscape Multibosyでシミュレーションした結果が同じになれば,運動方程式は正しそうという目処が立ちます.
余談ですが,Simscape Multibodyで運動が完璧にわかるのなら運動方程式を導出しなくてもいいのでは??と思う人がいるかも知れません. 実はそんなことはなくて,制御設計をする上では運動方程式は非常に重要になります.運動方程式が欲しいから,導出した運動方程式が正しいかをSimscape Multibodyで検証するといったイメージです.
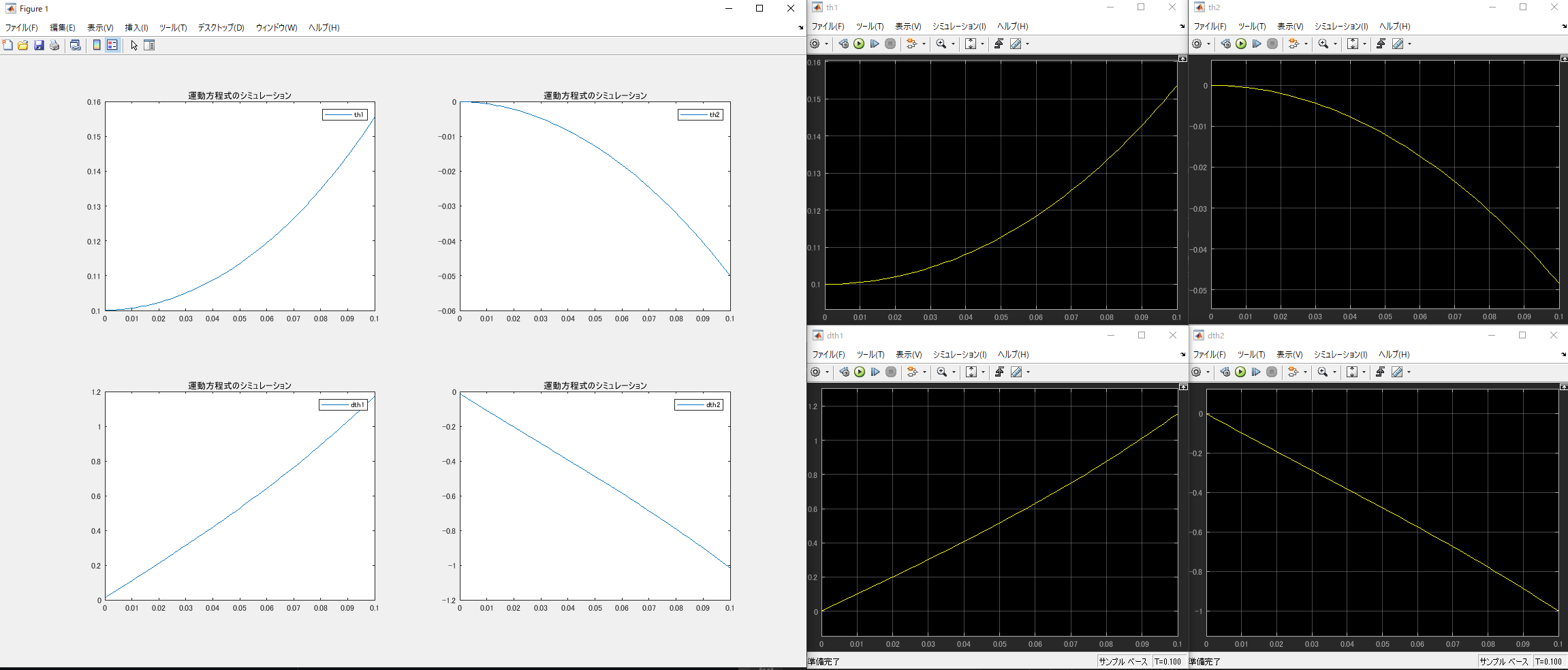
さて,それでは運動方程式を数値シミュレーションした結果とSimscape Multibodyでシミュレーションした結果を比較してみます. 線形化をしているので,$\theta_{1}$が小さいところだけを比較してみます.$\theta_{1}$の初期値を0.1[rad]にして,0.1[s]間に$\theta_{1}$, $\dot\theta_{1}$, $\theta_{2}$, $\dot\theta_{2}$ がどのように運動するかをシミュレーションしてみます.重力の影響でだんだんと角度と角速度が大きくなっていくはずです. 結果は以下のグラフのようになりました.左の4つのグラフが運動方程式のシミュレーション結果で,右の4つのグラフがSimscape Multibodyでシミュレーションしたグラフです. グラフの縦横比が若干違うのでわかりにくいですが,一致しました.この他にもいろいろな条件で比較しましたが,どれも一致しました.これで運動方程式が正しそうということがわかりました.
状態方程式の導出
正しそうな運動方程式がわかったので,いよいよ制御側の話に入ります.今回は現代制御の状態フィードバックで制御したいと思います.
まず運動方程式を状態方程式に変換します.状態変数は$[\theta_{1} \, \theta_{2} \, \dot\theta_{1} \, \dot\theta_{2}] ^T$にしました.
手計算で変換してもいいですが,これも間違える自信があるのでMATLABでやります.このスクリプトで変換しました.
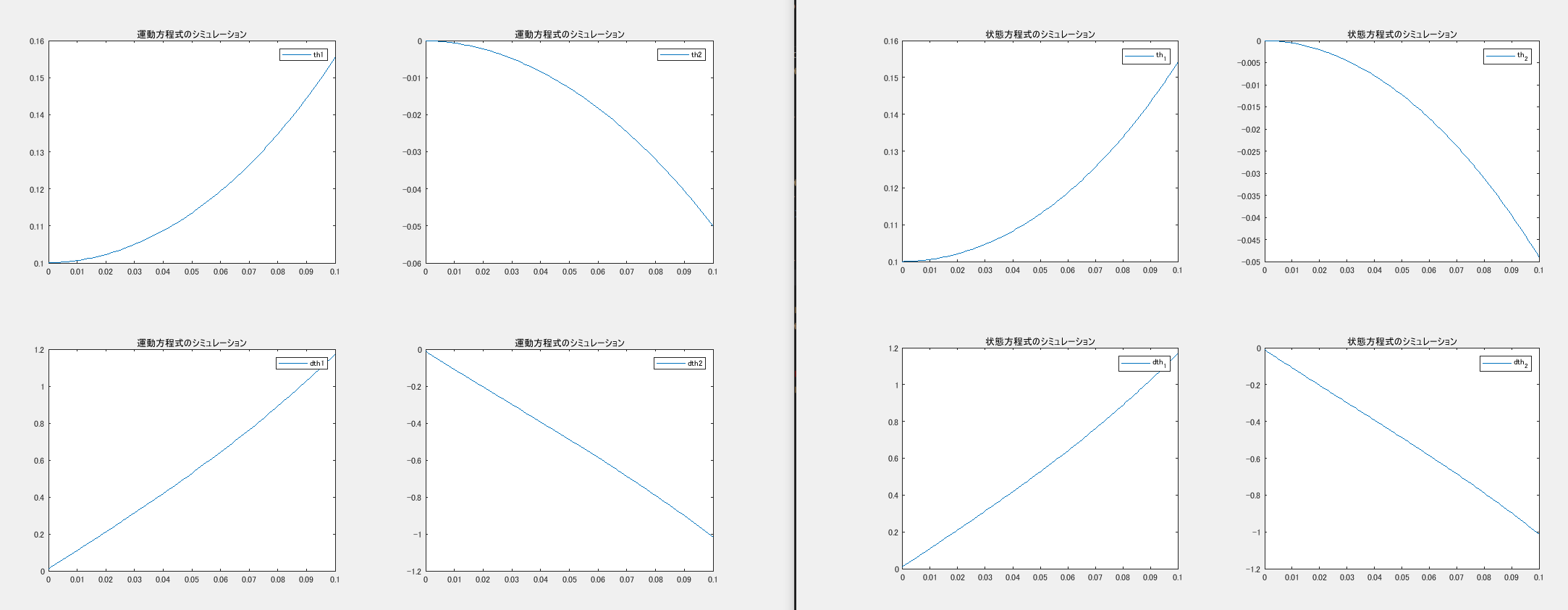
また,MATLABを使っても間違えていたらいけないので,状態方程式の形でもう一度数値シミュレーションをして,運動方程式のときと同じ結果になるかを確認しました.
結果は以下のグラフの様になり,同じだったので間違えていなそうです.
状態方程式は以下のようになりました.数式を書く気力がなかったのでスクリプトで勘弁してください.また,可制御性と可観測性は,共に可制御・可観測でした(可観測性は必要ない気もしますが一応).
M1 = (-c1/(m2*l^2 + m1*l_g^2 + I1));
M2 = (c2/(m2*l^2 + m1*l_g^2 + I1));
M3 = (g*(l*m2 + l_g*m1))/(m2*l^2 + m1*l_g^2 + I1);
M4 = 1/(m2*l^2 + m1*l_g^2 + I1);
M5 = (c1/(m2*l^2 + m1*l_g^2 + I1));
M6 = (-((c2*m2*l^2)/I2 + (c2*m1*l_g^2)/I2 + c2 + (I1*c2)/I2)/(m2*l^2 + m1*l_g^2 + I1));
M7 = (-g*(l*m2 + l_g*m1))/(m2*l^2 + m1*l_g^2 + I1);
M8 = (-((m2*l^2)/I2 + (m1*l_g^2)/I2 + I1/I2 + 1)/(m2*l^2 + m1*l_g^2 + I1));
A = [0, 0, 1, 0;
0, 0, 0, 1;
M3, 0, M1, M2;
M7, 0, M5, M6];
B = [0; 0; M4; M8];
C = [1, 1, 0, 0];
D = 0;
サーボ系の構築と状態フィードバックゲインを求める
必要ないと思いますが,サーボ系を構築しておきます.フライホイールの角度を指定できるようになります(本当にいらない). A行列とB行列を以下のよう変形します.変形後も可制御でした.
Ab = [A, zeros(4, 1);
-C, 0];
Bb = [B; 0];
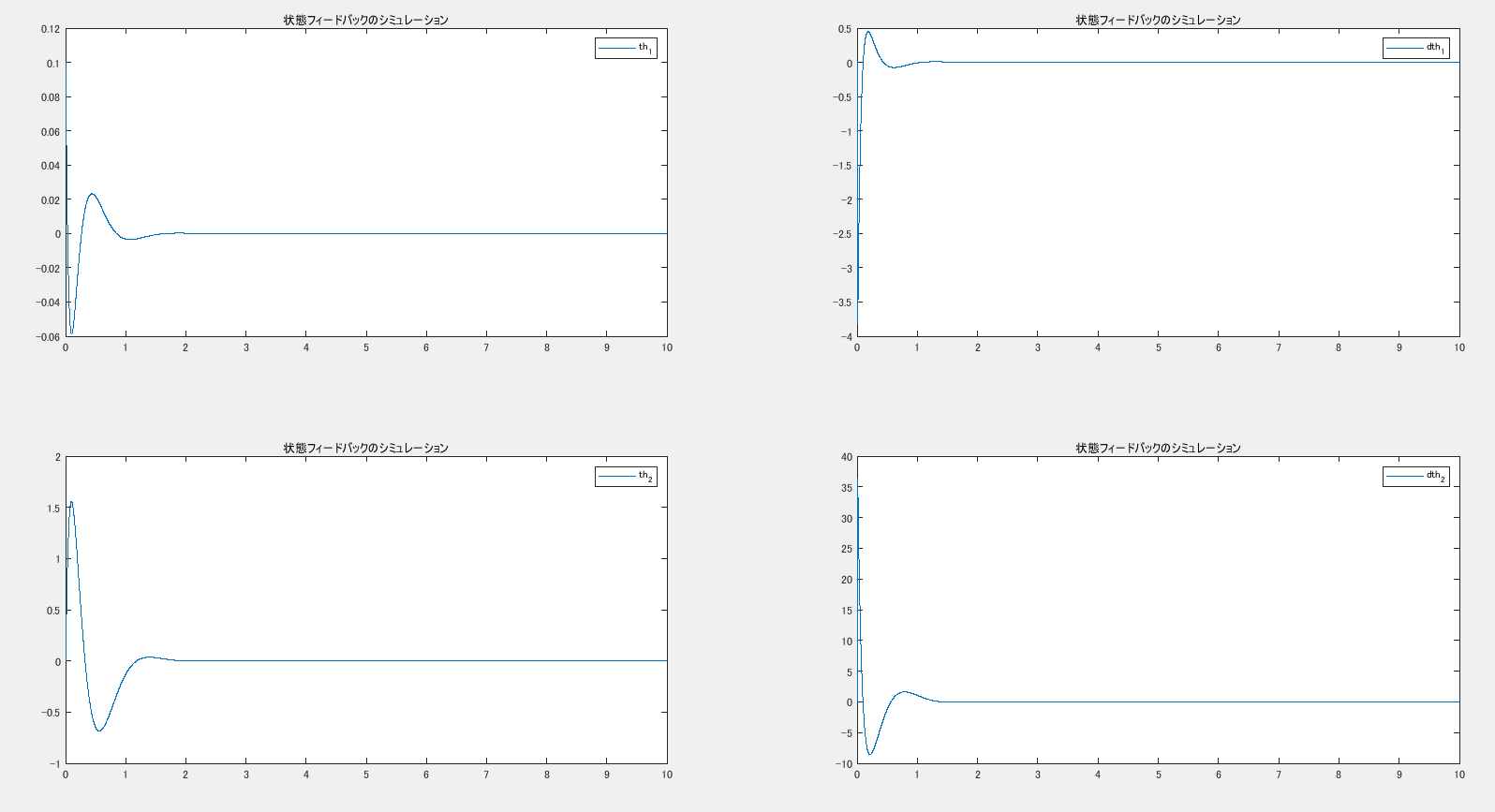
サーボ系を構築したら状態フィードバックゲインを求めます.今回は最適レギュレータを用いてゲインを決定します. こんな感じのスクリプトで求めました. 求めたゲインで状態フィードバックをシミュレーションしてみたら,以下のようにちゃんと収束しました.どうやらちゃんと制御できていそうです.
Simscape Multibodyでもシミュレーション
正直やる必要はないですが,動いている感が出てテンションが上がるのでやります.ファイルはこれです. そのまま実行すれば以下の動画のように倒立するはずです.
まとめ
フライホイール倒立振子の運動方程式を導出して,Simscape Multibodyで運動方程式の妥当性を検証し,状態フィードバックで倒立させました. 今回はSimscape Multibodyを運動方程式の妥当性の確認に使用しましたが,もっと複雑な構成をしている機械の動きを確認する用途でも本領を発揮するツールだと思います. なんにせよ非常に強力で便利なツールなので,みんな使いましょう!!
明日は@kaizen_nagoya さんの記事です.お楽しみに!


コメント
コメントを投稿